Gaussian Process Classification (GPC)

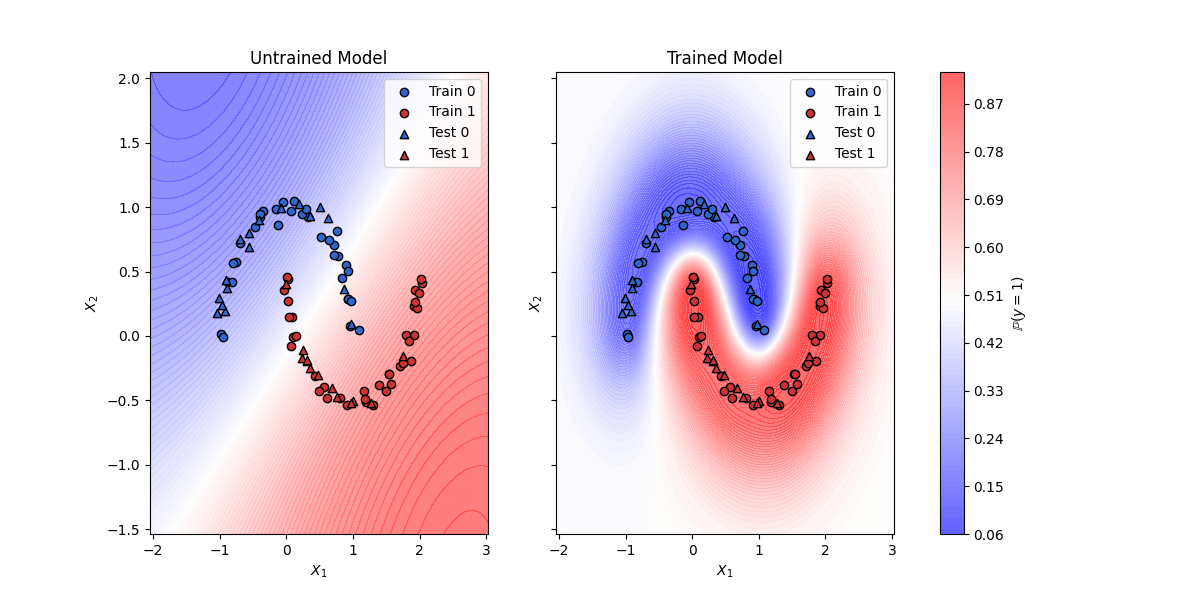
This script demonstrates the use of a Gaussian Process Classification (GPC) model with a the RBF kernel on generated data. The model is trained using the Adam optimizer to obtain optimal hyperparameters. The final model is compared against the untrained model.

• 
• 

Epoch: 1 - Log marginal likelihood: -39.296463691329514 - Parameters: {'rbf_sigma_4': 1.1, 'rbf_corr_len_4': 2.9}
Epoch: 11 - Log marginal likelihood: -31.227045988730723 - Parameters: {'rbf_sigma_4': 2.049, 'rbf_corr_len_4': 1.897}
Epoch: 21 - Log marginal likelihood: -19.423781982601678 - Parameters: {'rbf_sigma_4': 2.835, 'rbf_corr_len_4': 0.832}
Epoch: 31 - Log marginal likelihood: -14.168036564803643 - Parameters: {'rbf_sigma_4': 3.529, 'rbf_corr_len_4': 0.408}
Epoch: 41 - Log marginal likelihood: -13.806891876407672 - Parameters: {'rbf_sigma_4': 4.076, 'rbf_corr_len_4': 0.602}
Epoch: 51 - Log marginal likelihood: -13.017060182885137 - Parameters: {'rbf_sigma_4': 4.523, 'rbf_corr_len_4': 0.405}
Epoch: 61 - Log marginal likelihood: -12.552655775961789 - Parameters: {'rbf_sigma_4': 4.872, 'rbf_corr_len_4': 0.526}
Epoch: 71 - Log marginal likelihood: -12.281260688401275 - Parameters: {'rbf_sigma_4': 5.177, 'rbf_corr_len_4': 0.472}
Epoch: 81 - Log marginal likelihood: -12.106033356637964 - Parameters: {'rbf_sigma_4': 5.444, 'rbf_corr_len_4': 0.495}
Epoch: 91 - Log marginal likelihood: -11.969273182133417 - Parameters: {'rbf_sigma_4': 5.688, 'rbf_corr_len_4': 0.495}
Epoch: 101 - Log marginal likelihood: -11.85559005867789 - Parameters: {'rbf_sigma_4': 5.915, 'rbf_corr_len_4': 0.495}
Epoch: 111 - Log marginal likelihood: -11.75843894457935 - Parameters: {'rbf_sigma_4': 6.129, 'rbf_corr_len_4': 0.502}
Epoch: 121 - Log marginal likelihood: -11.674173383177472 - Parameters: {'rbf_sigma_4': 6.331, 'rbf_corr_len_4': 0.501}
Epoch: 131 - Log marginal likelihood: -11.600316034240281 - Parameters: {'rbf_sigma_4': 6.524, 'rbf_corr_len_4': 0.506}
Epoch: 141 - Log marginal likelihood: -11.534990046573588 - Parameters: {'rbf_sigma_4': 6.708, 'rbf_corr_len_4': 0.506}
Epoch: 151 - Log marginal likelihood: -11.476771185196467 - Parameters: {'rbf_sigma_4': 6.885, 'rbf_corr_len_4': 0.509}
Epoch: 161 - Log marginal likelihood: -11.424545187726945 - Parameters: {'rbf_sigma_4': 7.055, 'rbf_corr_len_4': 0.51}
Epoch: 171 - Log marginal likelihood: -11.377429515819294 - Parameters: {'rbf_sigma_4': 7.219, 'rbf_corr_len_4': 0.513}
Epoch: 181 - Log marginal likelihood: -11.334711322123908 - Parameters: {'rbf_sigma_4': 7.377, 'rbf_corr_len_4': 0.514}
Epoch: 191 - Log marginal likelihood: -11.295807368869834 - Parameters: {'rbf_sigma_4': 7.53, 'rbf_corr_len_4': 0.516}
Trained model test accuracy: 1.0
Untrained model test accuracy: 0.8999999761581421

import torch
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs, make_classification, make_moons
from copy import deepcopy

from DLL.MachineLearning.SupervisedLearning.GaussianProcesses import GaussianProcessClassifier
from DLL.MachineLearning.SupervisedLearning.Kernels import RBF, Linear, Matern, RationalQuadratic
from DLL.Data.Preprocessing import data_split
from DLL.Data.Metrics import accuracy
from DLL.DeepLearning.Optimisers import ADAM


n_samples = 100
dataset = "moons"
if dataset == "basic": X, y = make_blobs(n_samples=n_samples, n_features=2, cluster_std=1, centers=2, random_state=3)
if dataset == "narrow": X, y = make_classification(n_samples=n_samples, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, n_classes=2, random_state=4)
if dataset == "moons": X, y = make_moons(n_samples=n_samples, noise=0.05, random_state=0)
X = torch.from_numpy(X)
y = torch.from_numpy(y).to(X.dtype)

X_train, y_train, _, _, X_test, y_test = data_split(X, y, train_split=0.7, validation_split=0.0)

# untrained_model = GaussianProcessClassifier(RBF(correlation_length=torch.tensor([1.0, 1.0])), n_iter_laplace_mode=50)  # anisotropic kernel (each coordinate has different length scale)
untrained_model = GaussianProcessClassifier(RBF(correlation_length=3), n_iter_laplace_mode=50)  # isotropic kernel (each coordinate has the same length scale)
model = deepcopy(untrained_model)
untrained_model.fit(X_train, y_train)
model.fit(X_train, y_train)

optimizer = ADAM(0.1)  # make the learning rate a little larger than default as 0.001 takes a long time to converge. Could increase even more if wanted the true optimum for the sigma as well.
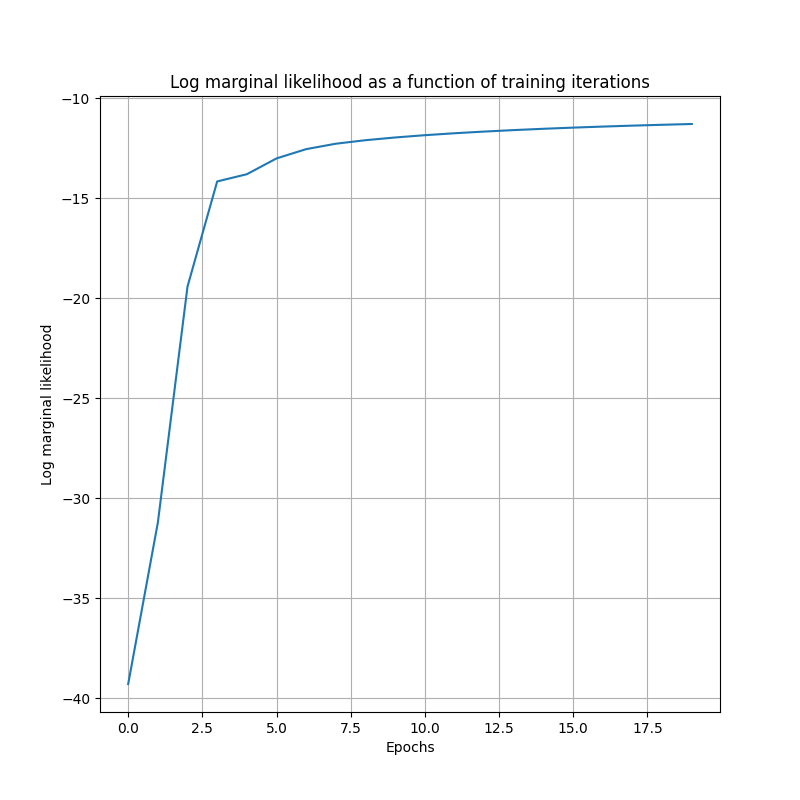
lml = model.train_kernel(epochs=200, optimiser=optimizer, callback_frequency=10, verbose=True)["log marginal likelihood"]

y_pred = model.predict(X_test)
print("Trained model test accuracy:", accuracy(y_pred, y_test))
y_pred = untrained_model.predict(X_test)
print("Untrained model test accuracy:", accuracy(y_pred, y_test))


x_min, x_max = X[:, 0].min() - 1.0, X[:, 0].max() + 1.0
y_min, y_max = X[:, 1].min() - 1.0, X[:, 1].max() + 1.0
n = 75
xx, yy = torch.meshgrid(torch.linspace(x_min, x_max, n, dtype=X.dtype),
                        torch.linspace(y_min, y_max, n, dtype=X.dtype), indexing='ij')
grid = torch.stack([xx.ravel(), yy.ravel()], dim=1)

with torch.no_grad():
    proba_untrained = untrained_model.predict_proba(grid).reshape(xx.shape)
    proba_trained = model.predict_proba(grid).reshape(xx.shape)

fig, axs = plt.subplots(1, 2, figsize=(12, 6), sharex=True, sharey=True)
blue = "#3366cc"
red = "#cc3333"
for ax, proba, title in zip(
    axs, [proba_untrained, proba_trained], ["Untrained", "Trained"]
):
    contour = ax.contourf(xx.numpy(), yy.numpy(), proba.numpy(), levels=100, cmap="bwr", alpha=0.7, vmin=0, vmax=1)
    ax.scatter(X_train[y_train == 0, 0], X_train[y_train == 0, 1], c=blue, edgecolor='k', label='Train 0')
    ax.scatter(X_train[y_train == 1, 0], X_train[y_train == 1, 1], c=red, edgecolor='k', label='Train 1')
    ax.scatter(X_test[y_test == 0, 0], X_test[y_test == 0, 1], c=blue, edgecolor='k', marker='^', label='Test 0')
    ax.scatter(X_test[y_test == 1, 0], X_test[y_test == 1, 1], c=red, edgecolor='k', marker='^', label='Test 1')
    ax.set_title(f"{title} Model")
    ax.set_xlabel("$X_1$")
    ax.set_ylabel("$X_2$")
    ax.legend()

fig.colorbar(contour, ax=axs.ravel().tolist(), label="$\\mathbb{P}(y = 1)$")

plt.figure(figsize=(8, 8))
plt.plot(lml.numpy())
plt.title("Log marginal likelihood as a function of training iterations")
plt.ylabel("Log marginal likelihood")
plt.xlabel("Epochs")
plt.grid()

plt.show()