Gaussian Process Regressor (GPR)

This script demonstrates the use of a custom Gaussian Process Regressor (GPR) model with a compound kernel on generated data. The model is trained using a combination of a linear kernel and a periodic kernel, and the training process optimizes the kernel parameters to fit the data. The script also compares the custom GPR model with the GPR implementation from Scikit-learn using a different kernel combination.

• 
• 

Epoch: 1 - Log marginal likelihood: -132.37171507706094 - Parameters: {'linear_sigma_4': 0.21, 'linear_sigma_bias_4': 1.01, 'periodic_sigma_1': 0.99, 'periodic_corr_len_1': 2.01, 'periodic_period_1': 0.49, 'white_gaussian_sigma_2': 0.99}
Epoch: 26 - Log marginal likelihood: -95.96261976434381 - Parameters: {'linear_sigma_4': 0.454, 'linear_sigma_bias_4': 1.265, 'periodic_sigma_1': 0.914, 'periodic_corr_len_1': 2.035, 'periodic_period_1': 0.337, 'white_gaussian_sigma_2': 0.725}
Epoch: 51 - Log marginal likelihood: -79.99508791980072 - Parameters: {'linear_sigma_4': 0.63, 'linear_sigma_bias_4': 1.437, 'periodic_sigma_1': 1.054, 'periodic_corr_len_1': 2.068, 'periodic_period_1': 0.329, 'white_gaussian_sigma_2': 0.476}
Epoch: 76 - Log marginal likelihood: -78.68354817718819 - Parameters: {'linear_sigma_4': 0.757, 'linear_sigma_bias_4': 1.487, 'periodic_sigma_1': 1.103, 'periodic_corr_len_1': 2.205, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.47}
Epoch: 101 - Log marginal likelihood: -78.05249440305616 - Parameters: {'linear_sigma_4': 0.851, 'linear_sigma_bias_4': 1.475, 'periodic_sigma_1': 1.153, 'periodic_corr_len_1': 2.372, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.466}
Epoch: 126 - Log marginal likelihood: -77.67368785663058 - Parameters: {'linear_sigma_4': 0.925, 'linear_sigma_bias_4': 1.431, 'periodic_sigma_1': 1.221, 'periodic_corr_len_1': 2.527, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.467}
Epoch: 151 - Log marginal likelihood: -77.42478827960053 - Parameters: {'linear_sigma_4': 0.985, 'linear_sigma_bias_4': 1.369, 'periodic_sigma_1': 1.281, 'periodic_corr_len_1': 2.677, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.465}
Epoch: 176 - Log marginal likelihood: -77.24818060019139 - Parameters: {'linear_sigma_4': 1.033, 'linear_sigma_bias_4': 1.293, 'periodic_sigma_1': 1.338, 'periodic_corr_len_1': 2.812, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.465}
Epoch: 201 - Log marginal likelihood: -77.11313270696806 - Parameters: {'linear_sigma_4': 1.074, 'linear_sigma_bias_4': 1.207, 'periodic_sigma_1': 1.388, 'periodic_corr_len_1': 2.931, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.465}
Epoch: 226 - Log marginal likelihood: -77.00225390698513 - Parameters: {'linear_sigma_4': 1.109, 'linear_sigma_bias_4': 1.111, 'periodic_sigma_1': 1.431, 'periodic_corr_len_1': 3.033, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.465}
Epoch: 251 - Log marginal likelihood: -76.90511873575224 - Parameters: {'linear_sigma_4': 1.138, 'linear_sigma_bias_4': 1.007, 'periodic_sigma_1': 1.466, 'periodic_corr_len_1': 3.119, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.465}
Epoch: 276 - Log marginal likelihood: -76.81502012716703 - Parameters: {'linear_sigma_4': 1.164, 'linear_sigma_bias_4': 0.896, 'periodic_sigma_1': 1.494, 'periodic_corr_len_1': 3.189, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.465}
Epoch: 301 - Log marginal likelihood: -76.72722825251026 - Parameters: {'linear_sigma_4': 1.187, 'linear_sigma_bias_4': 0.777, 'periodic_sigma_1': 1.515, 'periodic_corr_len_1': 3.245, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.465}
Epoch: 326 - Log marginal likelihood: -76.63794335993951 - Parameters: {'linear_sigma_4': 1.208, 'linear_sigma_bias_4': 0.649, 'periodic_sigma_1': 1.53, 'periodic_corr_len_1': 3.288, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.465}
Epoch: 351 - Log marginal likelihood: -76.5436137505214 - Parameters: {'linear_sigma_4': 1.229, 'linear_sigma_bias_4': 0.513, 'periodic_sigma_1': 1.538, 'periodic_corr_len_1': 3.319, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.465}
Epoch: 376 - Log marginal likelihood: -76.44092263707951 - Parameters: {'linear_sigma_4': 1.249, 'linear_sigma_bias_4': 0.368, 'periodic_sigma_1': 1.542, 'periodic_corr_len_1': 3.342, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.465}
Epoch: 401 - Log marginal likelihood: -76.3312782932224 - Parameters: {'linear_sigma_4': 1.272, 'linear_sigma_bias_4': 0.217, 'periodic_sigma_1': 1.54, 'periodic_corr_len_1': 3.358, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.464}
Epoch: 426 - Log marginal likelihood: -76.24744924744661 - Parameters: {'linear_sigma_4': 1.3, 'linear_sigma_bias_4': 0.089, 'periodic_sigma_1': 1.533, 'periodic_corr_len_1': 3.375, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.464}
Epoch: 451 - Log marginal likelihood: -76.20495920609369 - Parameters: {'linear_sigma_4': 1.336, 'linear_sigma_bias_4': 0.062, 'periodic_sigma_1': 1.528, 'periodic_corr_len_1': 3.387, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.464}
Epoch: 476 - Log marginal likelihood: -76.17377139889655 - Parameters: {'linear_sigma_4': 1.368, 'linear_sigma_bias_4': 0.051, 'periodic_sigma_1': 1.531, 'periodic_corr_len_1': 3.392, 'periodic_period_1': 0.331, 'white_gaussian_sigma_2': 0.464}

import torch
import matplotlib.pyplot as plt
from sklearn.gaussian_process import GaussianProcessRegressor as GPR
from sklearn.gaussian_process.kernels import DotProduct, ExpSineSquared, ConstantKernel, Matern as sk_matern, WhiteKernel

from DLL.MachineLearning.SupervisedLearning.GaussianProcesses import GaussianProcessRegressor
from DLL.MachineLearning.SupervisedLearning.Kernels import RBF, Linear, WhiteGaussian, Periodic, RationalQuadratic, Matern
from DLL.DeepLearning.Optimisers import ADAM
from DLL.Data.Preprocessing import StandardScaler


torch.manual_seed(0)
# device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
device = torch.device("cpu")
n = 100
# X = torch.linspace(0, 1, n, dtype=torch.float64, device=device).unsqueeze(1)
X = torch.rand(size=(n,), dtype=torch.float64, device=device).unsqueeze(1)
Y = torch.sin(3 * 2 * torch.pi * X) + 3 * X ** 2 + torch.randn_like(X) * 0.5
transformer = StandardScaler()
Y = transformer.fit_transform(Y).squeeze(dim=1)

train_kernel = True  # try to changing this line of code to see how the covariance kernel learns the correct parameters

# WhiteGaussian kernel is quite important as without it, the noise of the model has to be a lot larger.
model = GaussianProcessRegressor(Linear(sigma=0.2, sigma_bias=1) ** 2 + Periodic(1, 2, period=0.5) + WhiteGaussian(), noise=0.001, device=device)
sk_model = GPR(ConstantKernel(constant_value=0.2, constant_value_bounds=(1e-6, 1e1)) * DotProduct(sigma_0=1) ** 2 + ExpSineSquared(length_scale_bounds=(1e-6, 1e1)) + WhiteKernel())
model.fit(X, Y)
if train_kernel:
    history = model.train_kernel(epochs=500, optimiser=ADAM(0.01), callback_frequency=25, verbose=True)
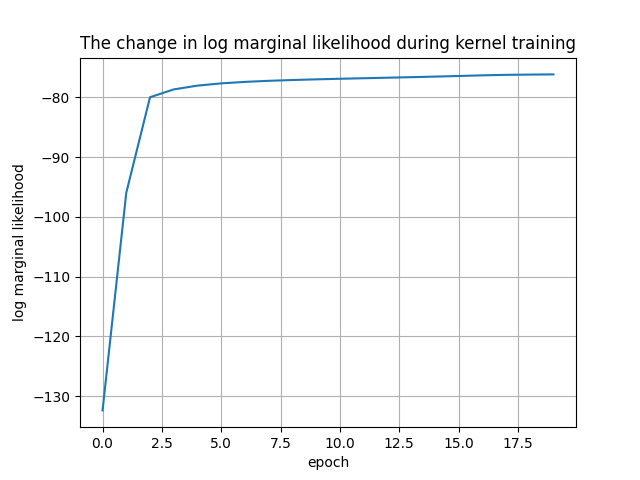
    plt.plot(history["log marginal likelihood"])
    plt.xlabel("epoch")
    plt.ylabel("log marginal likelihood")
    plt.title("The change in log marginal likelihood during kernel training")
    plt.grid()

sk_model.fit(X, Y)

x_test = torch.linspace(0, 2, 100, dtype=torch.float64, device=device).unsqueeze(1)
mean, covariance = model.predict(x_test)
mean = mean.squeeze()
mean = transformer.inverse_transform(mean)
covariance = covariance * transformer.var ** 2
std = torch.sqrt(torch.diag(covariance))

# draw random samples from the distribution
blue_theme = [
    "#1f77b4",
    "#4a8cd3",
    "#005cbf",
    "#7cb9e8",
    "#0073e6",
    "#3b5998",
]
plt.rcParams["axes.prop_cycle"] = plt.cycler(color=blue_theme)

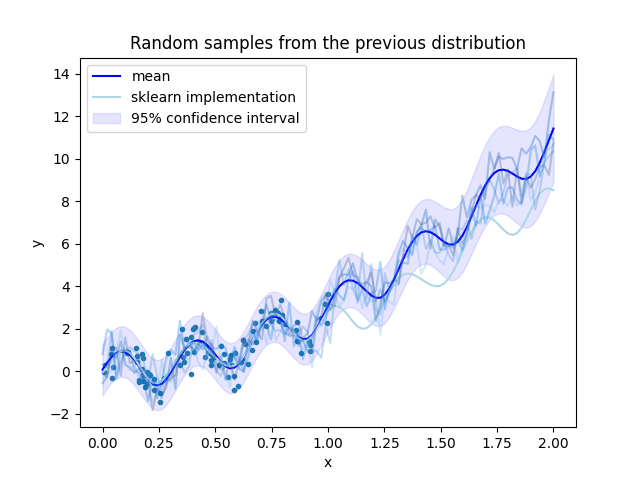
plt.figure()
plt.plot(X.cpu(), transformer.inverse_transform(Y).cpu(), ".")
plt.plot(x_test.cpu(), mean.cpu(), color="blue", label="mean")
plt.plot(x_test.cpu(), transformer.inverse_transform(torch.from_numpy(sk_model.predict(x_test.numpy()))), color="lightblue", label="sklearn implementation")
plt.fill_between(x_test.squeeze(dim=1).cpu(), mean.cpu() - 1.96 * std.cpu(), mean.cpu() + 1.96 * std.cpu(), alpha=0.1, color="blue", label=r"95% confidence interval")
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
plt.title("Predictions with the GPR model")

try:
    distribution = torch.distributions.MultivariateNormal(mean, covariance)
    for _ in range(5):
        y = distribution.sample()
        plt.plot(x_test.cpu(), y.cpu(), alpha=0.3)
    plt.xlabel("x")
    plt.ylabel("y")
    plt.title("Random samples from the previous distribution")
except:
    pass
finally:
    plt.show()